Solution:
We assume that a<b, let's observe various possible operations:
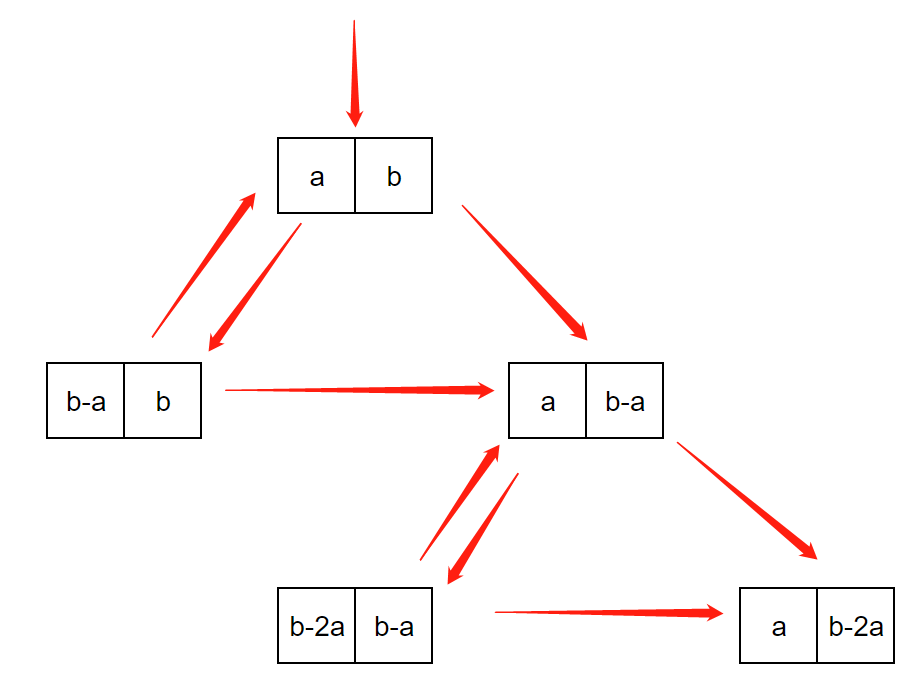
According to the above picture, we find that when 0<a<b-2a, a will never be replaced, and b will continue to be replaced by ba until there is a certain c such that b-(c+1)a<0 and b-ca>0.
Take the first step as an example, suppose we set a:=b-a. Then the second step is b-(b-a)=a. Then the result of second step is either (a, b) or (a, b-a).
In the same way, we find that only (a, b-a) can be further transformed into (a, b-2a), (a, b-3a)...
Then suppose such a c such that b-(c+1)a<0 and b-ca>0. During the process from (a, b) to (a, b-ca), the possible numbers are: a, b, b-a, b-2a, ..., b-ca. And obviously b-ca = b% a, so b-ca <a.
So we re-use (b% a, a) as the initial value, and search for x in all possible numbers again.
Code:
Java

C++

