Solution:
First of all, we can immediately find that for the grid (x, y), no matter how the robot moves, the parity of the grid x+y is always the same. So it is natural to solve for odd and even numbers separately.
Then we consider how the robot can move in order to minimize the number of times. It is conceivable that the robot must take it in order from left to right.
Take the following picture as an example, we can see that the robot takes the (3,3) candy first. But as a result, the candy on the left (3,1) must be taken again. This will take 3 times.
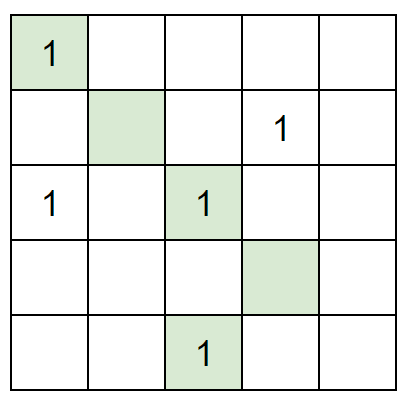
Therefore, the strategy in the above figure should become (only 2 times):
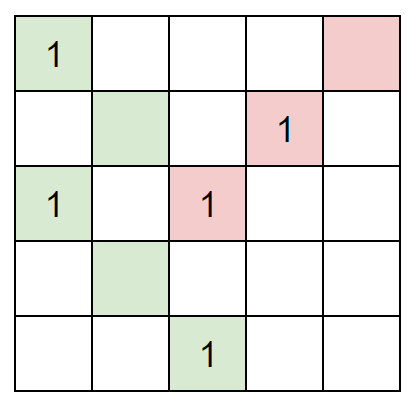
So we came to the conclusion that it must be taken from left to right. Now let us take the following figure as an example, consider the following question: Compared with (1, 6), are the green 1 and red 1 both on the left side of (1, 6)?
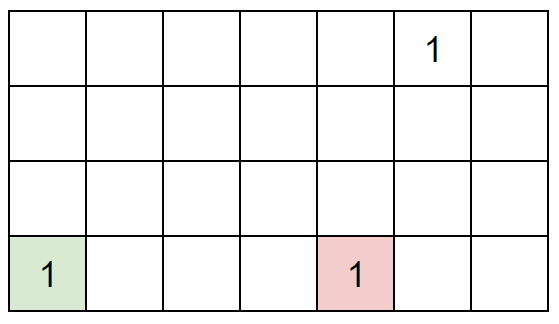
Starting from the yellow 1, we can see that the green 1 is actually more "left", while the red 1 is actually to the right of the yellow 1. As shown below:
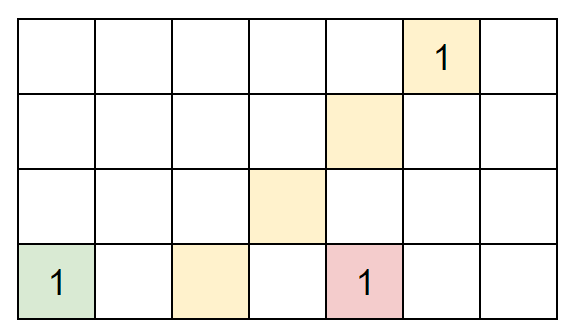
Therefore, according to the conclusion taken from left to right, we define right_top=y+x. So we only need to sort according to right_top to get the points sorted from left to right. That is to say, the smaller the right_top, the more it should be taken away first.
The final question is how many times it needs to take all candies according to this strategy. We found that in the above picture, the green 1 needs to be taken at one time, while the red 1 and yellow 1 can be taken at one time. Then we consider under when we can take candies together.
We define left_top=y-x. So we found that if and only if as x increases, right_top also increases, and left_top decreases, they can be taken together.
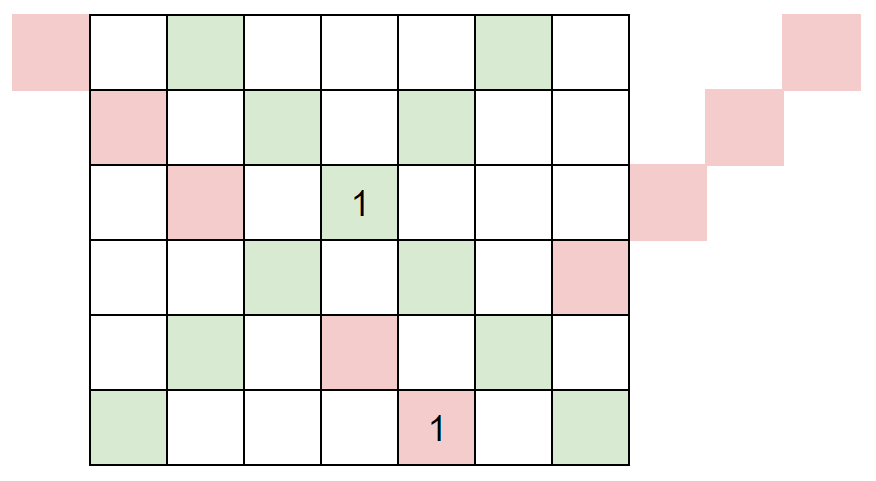
At the same time, we noticed that the larger the right_top-left_top, the larger the x. Therefore, as right_top increases, if left_top decreases, then this 1 must look like the red 1 in the above figure. And if left_top not only does not decrease or even increases, it must fall to the right of green 1, and cannot be taken together.
So, as right_top continues to move to the right (because we sort from small to large), we only need to check whether there is another 1 on the right side of its left_top each time. If there is, then the two 1s are taken together.
And the x of the 1 on the right must be smaller than the x of the current 1. Therefore, we adjust the left_top of the original 1 to the new left_top so that the subsequent 1s can continue processing.
Code:
Java

C++

