Solution:
First, because gcd(a,b,c) must be less than or equal to gcd(a,b) or gcd(b,c). Therefore, the maximum distance must be the largest side.
So it is not difficult to find that we query all the nodes for the first time and get the edge weight of the largest edge in the tree. Then binary search all edges. If this half of the edge contains the largest edge weight, then continue the binary search in this half, otherwise, the binary search in the other half.
The question now is how to find exactly half of the edges to query.
First of all, we notice that the final result must be two adjacent nodes, and the edge weight between these two nodes is the largest. And we can notice that one of the two adjacent nodes must be a son and the other is a father.
So we only need to find such a node, so that this node meets this condition: the edge weight between this node and the parent node of this node is the largest.
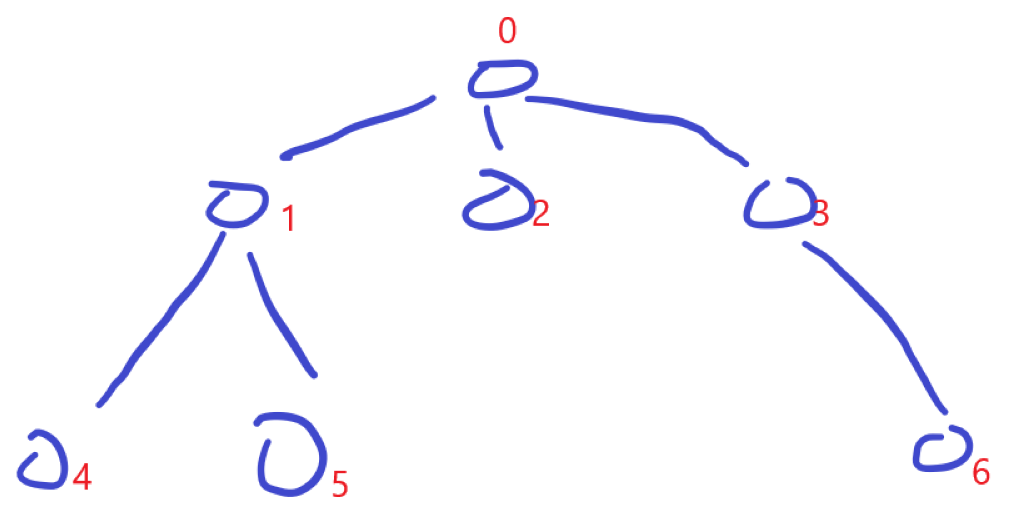
So it is very natural, we renumber all nodes in order from the root to the bottom (as shown in the figure below). We only need to perform a binary search in the range of [1,n-1] (obviously, we need to include the father of the target node when searching. For example, when the target is [1,2,3], we need to query [0, 1,2,3] the id of these 4 nodes).
Code:
Java

C++

