A. CQXYM Count Permutations
Solution:
It is not difficult to think that there are x of i satisfying the condition in an permutations , then if we reverse the permutations, there are 2n-x of i satisfying the condition. For example, [3,2,1,4]=1, then [4,1,2,3]=4-1=3.
Therefore, the number of i that meet the conditions is actually evenly distributed. So the answer is $\frac {2n!} 2$.
Code:
Java

C++

B. Diameter of Graph
Solution:
Obviously, if m is less than n-1, not all points can be connected, and it must be NO. Similarly, if m is more than $\frac {n \cdot (n-1)} 2$, there must be a duplicate edge, which is also NO.
Obviously, if $k-1\leq 0$, which is the maximum allowable diameter $\leq -1$, it must be NO.
If $k-1=1$, that is, the diameter must be 0, YES if and only if n=1, otherwise NO.
But if $k-1\geq 3$, which is the diameter $\geq 2$, there must be a solution. We can give the structure of the following figure:
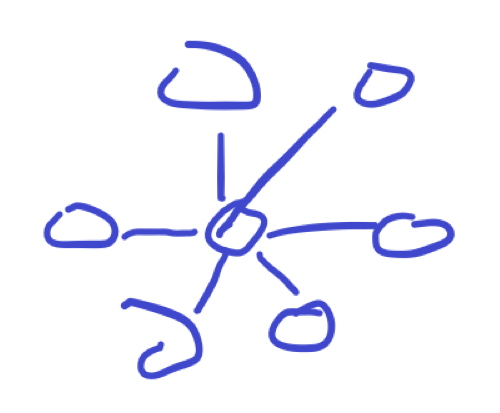
In the end, we only have $k-1=2$ left without consideration, that is, the diameter is 0 or 1.
For a diameter of 0, which has just been considered, n must be 1.
If the diameter is 1, there must be an edge between any two points, so YES if and only if $m=\frac {n \cdot (n-1)} 2$, otherwise NO.
Code:
Java

C++

C. Portal
The key to this question is to find that the final answer must be less than or equal to 16. Then brute force search based on this conclusion.
D. Mathematics Curriculum
The key to this question is: thinking of the maximum value of the interval as the boundary, the interval on the left and right of it does not affect each other at all. So can split sub-question based on this conclusion, and further DP is a natural choice.

E. Train Maintenance
The key to this problem is that the cases where the value of x[i]+x[y] is large and small can be handled separately. And believe that Codeforce can process 100 million calculations in a second.
