A. Gamer Hemose
Solution:
Obviously, we only need to choose the two weapons with the highest attack power to attack alternately.
Code:
Java

C++

B. Hemose Shopping
Solution:
Consider three numbers a[i], a[j], a[k]. Suppose i<j<k, and $j-i\geq x$. We can do the following to achieve any interchange of these three numbers:
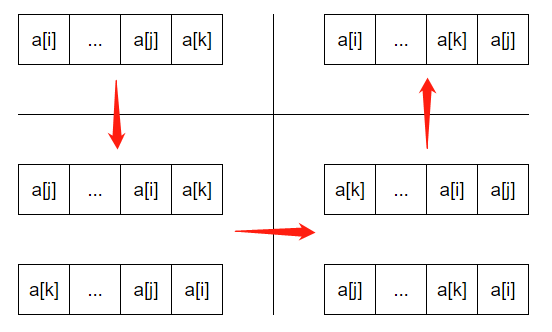
Therefore, if the two intervals [x, n-1] and [0, n-1-x] have an intersection, then there is no doubt that the entire array can be reordered.
If x>n-1, that is, there is no sortable interval, then the entire array cannot be reordered.
In the middle of the above two extreme cases, [x, n-1] and [0, n-1-x] can obviously be reordered separately. But considering that a[0] can be exchanged with a[n-1] at any time, so except that [n-1-x, x] cannot be sorted, other intervals can be sorted arbitrarily.
Combining the above three situations, we come to the conclusion that there are only [n-1-x, x] that cannot be sorted. (This interval may be an invalid interval, as in the first case. It may also be the entire array, as in the second case.)
We only need to see whether the subscript whose value changes after sorting belongs to the interval that cannot be sorted.
Code:
Java

C++

C. Bakry and Partitioning
This question is a typical application of one of XOR properties: a xor a = 0, 0 xor a = a.

D. Hemose in ICPC ?
The idea of this problem is easy to think of, which is an obvious binary search. But there is a clever way to find half of the edges every time.
Recently, I have been busy with work, and I really don’t have the time and energy to do the E question.