Solution:
First, we can note that: when i is odd number, f(i)=2.
Then we consider the case that f(i)=3. Based on the definition, if and only if i is even number and i cannot be divisible by 3, then f(i)=3.
So, we know that: for all the i, after excluded f(i)=2 and f(i)=3, the remain i cannot be divisible by 6.
Furthermore, after we excluded f(i)=4, the remain i cannot be divisible by lcm(4,6)=12.
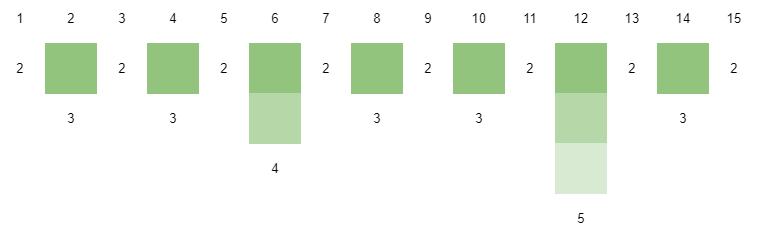
Based on the image above we can find that:
after f(i)=2, all the i remain match $i\equiv 0 (mod 2)$.
after f(i)=3, all the i remain match $i\equiv 0 (mod 6)$, which is 6 and 12. (where lcm(2,3)=6)
after f(i)=4, all the i remain match $i\equiv 0 (mod 12)$, which is 12 and 24. (where lcm(6,4)=12)
So, we just enumerate the value of f(i), we compare the number of remain i between two value every time.
So, the number of i where $f(i)=x$ is $\frac{n}{lcm(1,2,3,...x-1)}-\frac{n}{lcm(1,2,3,...,x)}$.
Code:
Java

C++

