A. Pretty Permutations
Solution:
Obviously, only the two neighbors need to exchange positions with each other.
For the case where n is an odd number, only the last three bits need to be exchanged with each other.
Code:
Java
Submission #120639795 - Codeforces
Codeforces. Programming competitions and contests, programming community

C++
Submission #120676730 - Codeforces
Codeforces. Programming competitions and contests, programming community

B. Pleasant Pairs
Solution:
Sort the original array a.
Then for any value, we can enumerate the a from small to large. We stop the enumeration when the product greater than 2n (i+j always less than 2n).
So, the time complexity is around $\frac{n}{a_1}+\frac{n}{a_2}+\frac{n}{a_3}+...\frac{n}{a_n}$.
Code:
Java
Submission #120641418 - Codeforces
Codeforces. Programming competitions and contests, programming community

C++
Submission #120676962 - Codeforces
Codeforces. Programming competitions and contests, programming community

C. Great Graphs
Solution:
To minimalize the positive value, we try to reuse the path which the cost is positive. So, the positive path looks like this:
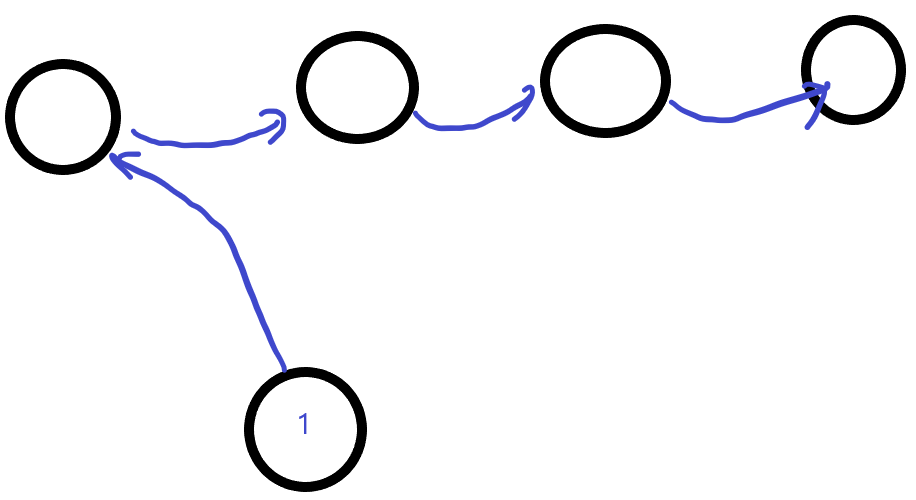
Then, to minimalize the negative path, we can build it based on the positive path:
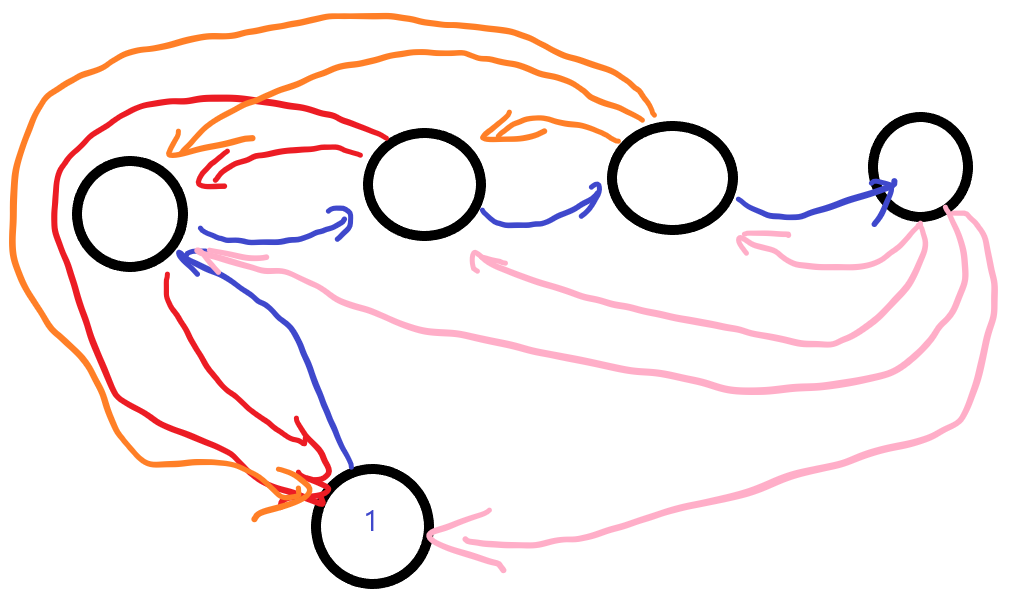
Code:
Java
Submission #120643726 - Codeforces
Codeforces. Programming competitions and contests, programming community

C++
Submission #120677095 - Codeforces
Codeforces. Programming competitions and contests, programming community



