A. Balanced Substring
Solution:
Just need to find "ab" or "ba" in the string.
Code:
Java

C++

B. Chess Tournament
Solution:
For those who don’t want to lose a game, we just keep them in a draw.
Those who want to win at least one game are left: as long as they can form a ring, there will be a solution. It should be noted that two people cannot form a ring.
Code:
Java

C++

C. Jury Meeting
Solution:
We find the person with the most tasks.
First, if there are multiple people, they all have the most tasks. So it is obvious that no matter how the arrangement is, the condition can be met. Just output n! directly.
If the person with the most tasks has more than two tasks (including two) than the person with the second most tasks, then it is obvious that there must be no solution.
Therefore, we are left with only one situation: a person with the most tasks, a number of people with the second most tasks, and others.
In this case, we only need to make sure that the person with the most tasks is followed by at least one person with the second most tasks.
Finally, insert others between the person with the most tasks and the person with the second most tasks.
Code:
Java

C++

D. Inconvenient Pairs
Solution:
It is not difficult to find that starting from a certain point, its inconvenient point must meet the following conditions:
- As shown by the red line in the figure below, this point must be between the nearest, two-sided, and vertical roads.
- As shown by the dotted line in the figure below, this point and the starting point are not on the same road.
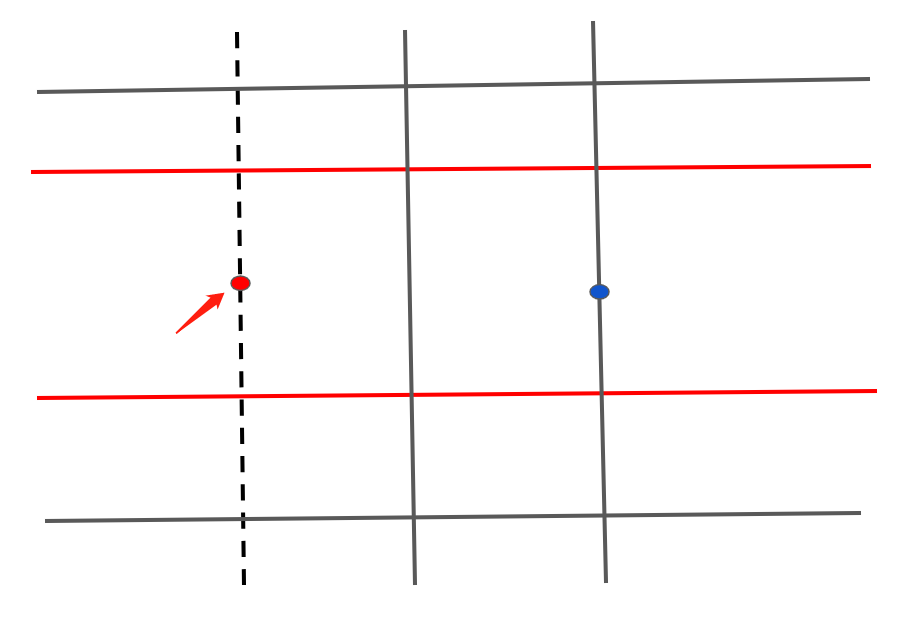
So obviously, we can find the point that satisfies the condition by binary search.
The difficulty of this question is that it requires multiple binary searches according to different conditions, so it is very troublesome to implement. Therefore, it is recommended to abstract all binary search into 1-2 functions, which is more convenient to implement.
Code:
Java

C++

