Solution:
First, we notice that the final result is only related to the maximum and minimum values of w. Which mean that as long as w is between the maximum and minimum values, whether or not this segment is added will not affect the result.
Therefore, we can immediately think that we sort all the segments according to w. We consider subtracting all the segments from both ends, until it will cause 1-m to not be fully covered if subtract again.
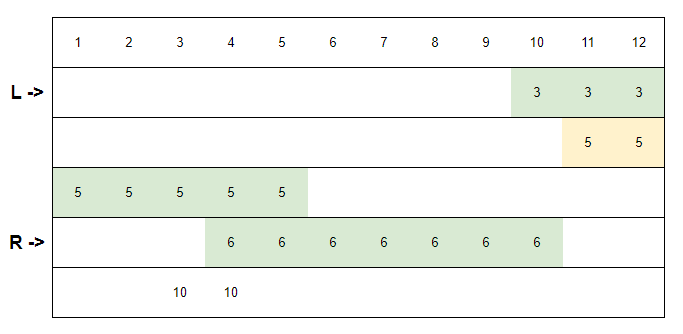
For example, we can see that this section of 11-12 (the yellow part) is actually optional and does not affect the result.
So in general, we move R down one place at a time, and then try to move L down until it just happens to be unable to move. This way we can quickly traverse all L and R pairs. Finally, we only need to take the minimum value of all w[R]-w[L].
Take the operation in the following figure as an example:
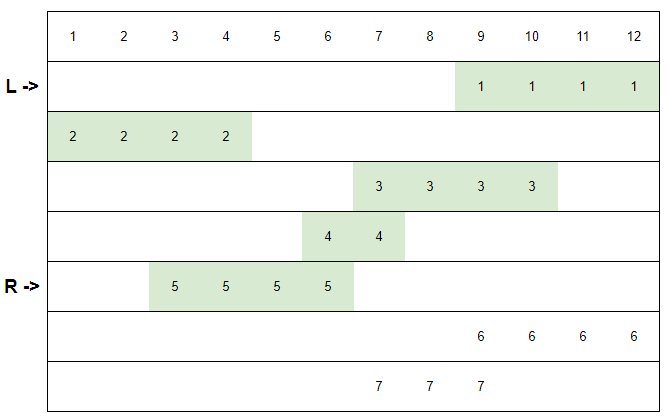
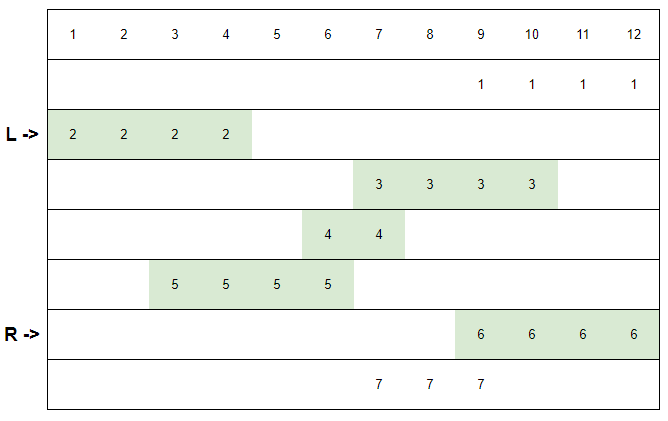
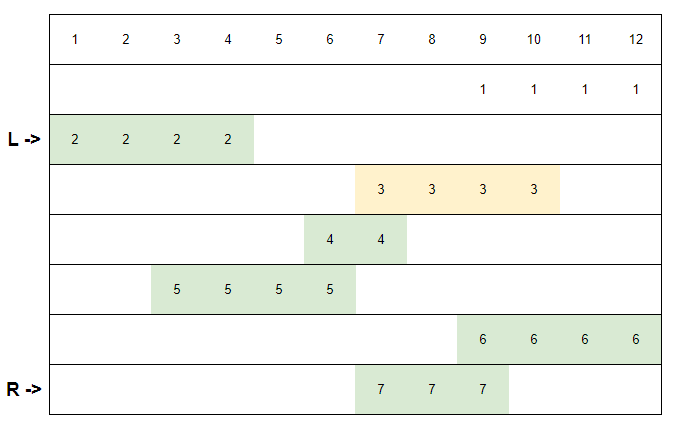
So the final question is how to quickly verify whether the segment between L and R can cover the entire 1-m. In fact, it is very obvious here, just use the segment tree to maintain.
When we add a segment into L and R, we update the correlation range with +1; when we remove it, we update the correlation range with -1. And because segment must be cross to each other, when we add or delete range, we put the range as left included and right not included.
Code:
Java

C++

