Solution:
First, let us pay attention to the range of l and r, $l\leq 1$, $r\geq n$. So, for the first half of a, you can let $a[i]=i+1$, and for the second half of a, you can let $a[i]=i-1$.
So, obviously, $F(a)=\left\lfloor \frac{m}{2} \right\rfloor \cdot \left\lceil \frac{m}{2} \right\rceil$.
Then, we can immediately discover that in fact, we can also let $a[i]=i\pm x$. x has $\min{(r-half, half+1-l)}$ possible values.

We also noticed that when n is an odd number, there is another possibility as shown in the figure below. Similarly, the number of possibilities is: $\min{(r-half-1, half+2-l)}$.
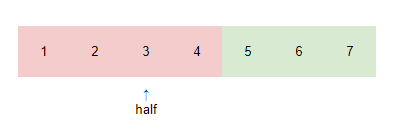
Before going further, let's give some definitions. We define the position of the rightmost +x as plus_pos, and the leftmost -x as minus_pos.
So we can conclude that for any permutation, the number of possibilities for the value of x is: $\min{(r-plus_pos, minus_pos-l)}$.

Next, let us consider the case where minus_pos is on the left of plus_pos, which looks like:
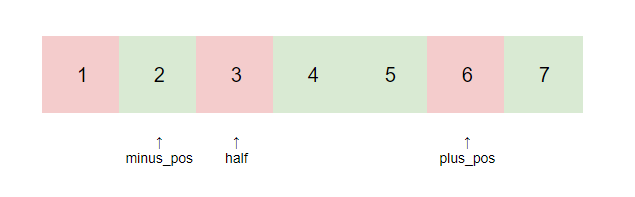
We can naturally think that we enumerate the positions of minus_pos and plus_pos. In this way, we only need to ensure $plus_pos \geq half$ and $minus_pos \leq half+1$.
For a certain pair of selected minus_pos and plus_pos, things in between can be arranged arbitrarily. Therefore, the number of permutations is: $$C_{plus\_pos\ -\ minus\_pos\ +\ 1}^{still\_need\_to\_plus}$$At the same time, because $${still\_need\_to\_plus}+{still\_need\_to\_minus}={plus\_pos\ -\ minus\_pos\ +\ 1}$$So, it's also equal to $$C_{plus\_pos\ -\ minus\_pos\ +\ 1}^{still\_need\_to\_minus}$$Where still_need_to_plus indicates the number of +x between minus_pos and plus_pos. Because the right side of plus_pos must be all -x, and the left side of minus_pos must be all +x, so$${still\_need\_to\_plus=n-(minus\_pos-1)-1}$$In the same way, we can give the definition and value of still_need_to_minus similarly.
Finally, we consider the number of possibilities for the value of x. So for a certain pair of selected minus_pos and plus_pos, the number of possibilities is:$$C_{plus\_pos\ -\ minus\_pos\ +\ 1}^{still\_need\_to\_plus} \cdot\min{(r-plus\_pos, minus\_pos-l)}$$
Unfortunately, the time complexity of enumerating the positions of minus_pos and plus_pos is $O(n^2)$. We still need to further optimize.
We can notice that for a specified plus_pos, when $minus_pos\geq r-plus_pos+l$, the number of possibilities for the value of x for each arrangement is always $r-plus_pos$.
Similarly, when minuns_pos is specified conversely, when $minus_pos\leq r-min_pos+l$, the number of possibilities for the value of x are $minus_pos-l$.
So we can consider separately according to the number of possibilities of x.
When the number of possibilities of x is $r-plus_pos$, as long as minus_pos meets the conditions, -x can choose the position arbitrarily. So the number of possibilities is:$$C_{plus\_pos\ -\ (r\ -\ plus\_pos\ +\ l)}^{still\_need\_to\_minus} \cdot (r-plus\_pos)$$
Take the following figure as an example, suppose we have selected plus_pos=6, and assuming $minus_pos\geq 2$, for any arrangement, the number of possibilities for x is always r-plus_pos. At this time, because minus_pos only needs to be greater than or equal to 2, and still_need_to_minus is 2 (assuming we think that there are 3 -x in total). So there can be a total of $C_4^2\cdot (r-plus_pos)$ possibilities.
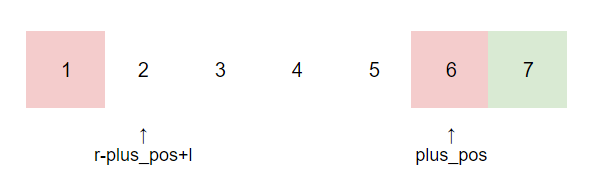
The situation of minus_pos-l is exactly the same.
Finally, we consider the parity of n.
When n is an even number, the number of +x and -x is always $\frac n 2$, so just follow the above solution directly.
When n is an odd number, the number of +x can be $\left\lfloor \frac{m}{2}\right\rfloor$, or $\left\lceil \frac{m}{2} \right\rceil$. Therefore, the two cases can be calculated according to the above solution and then summed.
Code:
Java

C++


