Solution:
First. Because the cost of child node must higher that their father node. So obviously, we will choose the shallower node. Then we need find the shallowest node which still have gold remained.
So, we naturally use binary search. Use a node which the level is 9. Multiplying to create an index of the position of its ancestor node. Like this:
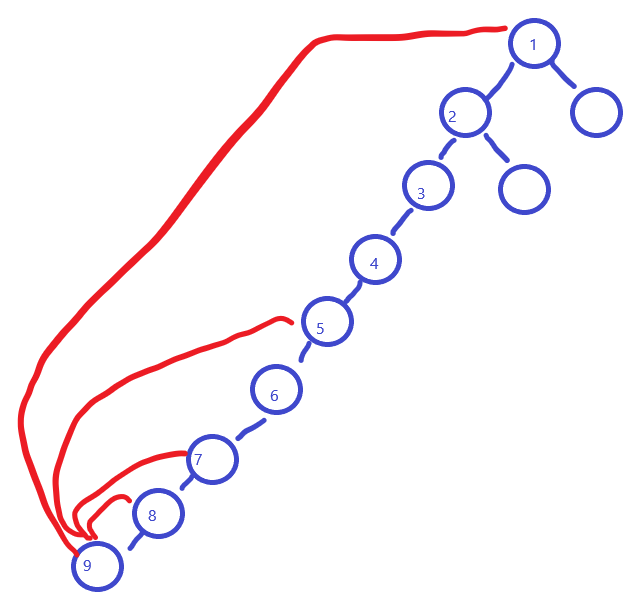
Let us assume the first node not have gold but 5th node has gold. But not sure if 2nd-4th node has gold or not, so we search from 5th node. And because 5th node also built the index. So, it looks like this:
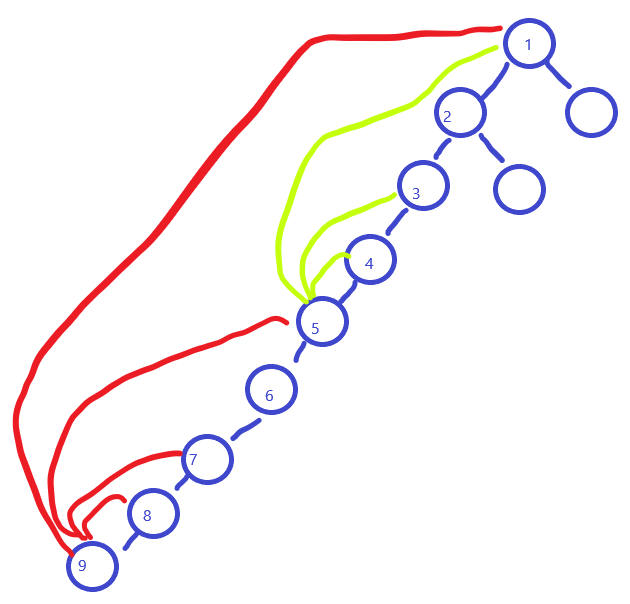
And so on, we can get the shallowest node which still have gold remained in O(logn). And we will buy gold on this node as much as possible. If the gold on this node is not enough, we buy all we can. And then find the shallowest node again from node 9.
But why this will not get TLE? Because for one query, the worst case is: if we only buy part of gold on some node, then the ancestor nodes' gold must already be bought by us, and the ancestor nodes must be empty.
So, if one of the nodes is empty, then all the ancestor nodes must be empty. So, even we will do the search multiple times. But except the last time, all the extra searches will only appear once (because after this time, the value must be 0. So will not appear again).
Code:
C++

Java
TLE on 26. But it is same solution with my C++ code. But only C++ can AC.


