Solution
First, for any two robots $i$ and $j$, if $x_i\equiv x_j\mod 2$ (the remainder of 2 is same), then these two robots must meet and explode somewhere. Otherwise, they will never meet each other.
Let us consider t seconds later, $x_i+t=m-1$. Of course $x_i+t\equiv x_j+t\mod 2$. And another 2 seconds later, we have $x_i+t\equiv x_i+t+2\equiv x_j+t \equiv x_j+t+2 \mod 2$.
So, if $x_i\equiv x_j\mod 2$, these two robots must can meet each other.
So, we split all the robots to two parts by the remainder of their starting coordinates divided by 2. For any part of the robots:
First, we consider the robot which is moving to right. There are two cases that this robot can explode:
1. there are robots which is moving to left, and the starting coordinates is on the right of this robot.
2. There are robots which is moving to right but not exploded.
The premise of these two cases is that: the robots from the right side was not meet any other robots before.
Consider the 2nd case we can find that: for the robot which turns to the left after turning around, the starting coordinates of it equal to $m+(m-x_i)$ and moving to left at beginning. (denote $m+(m-x_i)$ as realPos. The realPos equal to the $x_i$ if the robot is moving to left at the beginning.)
Also, we found that: the robot which turned around, it cannot find any robot meet with it from the right side. Maybe there is no robots on the right of it. Or maybe the robots on it right side already exploded.
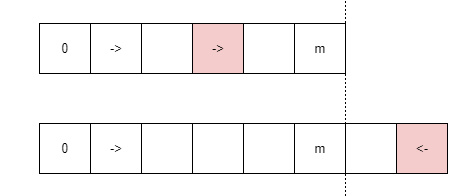
So, we check the robot from right to left one by one.
If this robot is moving to left. Then we put it into the priority queue and wait to pair with other robots moving to right.
If this robot is moving to right. Then we can find the most left robots by the realPos from priority, and this robot will meet with current robot. If no such robot, we calculate the realPos of current robot, and add current robot to the priority queue.
After all of this. we need manage the robots still in the priority queue.
Because all these robots are moving to left (include the robots turned around). So, they must can meet with each other two by two from left to right.
Code:
Java:

C++:


