Solution:
We consider the image of querying [x, n]. In other words, as x changes, the changes of the result of query (? x n) .
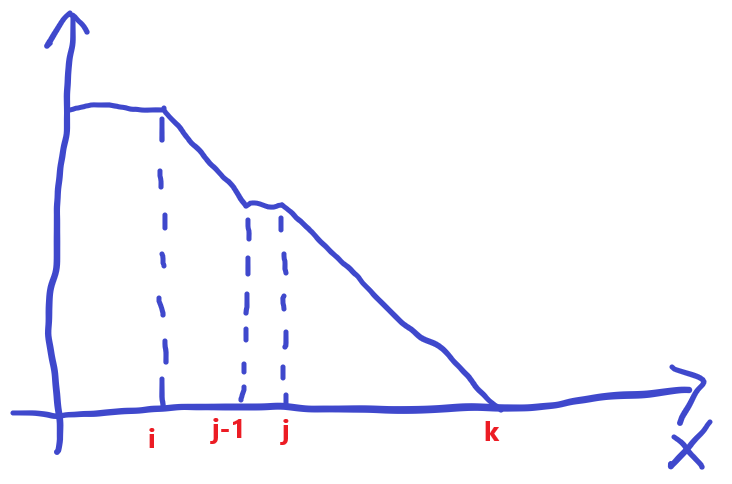
In other words, when $x\leq i$, (? x n)=(? 1 n). And when $x \geq k$, (? x n)=0.
And because x=j-1, because at this time a[j-1]<a[y] (where $j\leq y \leq k$), so (? j-1 n)=(? j n). Except for this, the images at other locations are strictly monotonically decreasing.
So obviously, i and k can be found by binary search.
But this will face two problems: 1. According to the scale of n, each binary search requires 30 queries, and searching for both i and k at the same time will require 60 queries. 2. How to find the value of j?
It is not difficult to find that when $x\geq j$, there must be an integer solution for y in $\text{(? x n)}=\frac {len\cdot (len -1)} 2$. When $x< j-1$, there is a high probability that y does not have an integer solution (taking i=1, j=10, k=12, x=7 as an example, (? 7 12)=6, and y is still has integer solutions, but this is a rare case).
Therefore, when we find that the y after a query has an integer solution, we can calculate the value of k based on x and y, k = x + y -1.
But considering the few cases mentioned above, we can judge by query (? x+y-2 x+y-1), if the query result is 1, then k=x+y-1. If the query result is 3, it may be x=j-1, so we can try again.
Similarly, when x=j, not only (? x n) has an integer solution, (? 1 n)-(? x n) must also have an integer solution, and (? x-1 n)=(? x n). When x=j-1, (? 1 n)-(? x n) must have an integer solution, and (? x-1 n)=(? x n) + 1.
So we can judge whether x is to the left of j-1 or to the right of j, or whether x is j or j-1.
Code:
Java

C++

