Solution:
We first consider when $u\oplus v> \min(u,v)$. It is not difficult to find that $u\oplus v> \min(u,v)$ if and only if one of the highest bits of u and v is 0 and the other is 1. Take the following picture as an example:
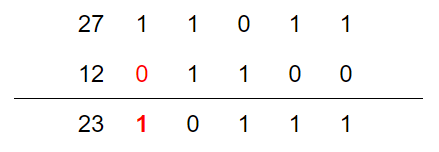
So we get a very important property: there are and only nodes with labels from $2^i$ to $2^{i+1}-1$ can move to each other. And this range has a total of $2^i$ nodes.
Therefore, we thought that we can use any point as the root of the tree and maintain the depth of each node. We can select several groups of numbers that can communicate with each other, and then we assign all these numbers to nodes with an odd depth. That is, the total number of these depth nodes must be exactly equal to the number of numbers we selected.
In this way, because you can only take one step at a time, choosing any node is sure to win.
For example, we selected two sets of numbers: $[2^0, 2^1-1]$ and $[2^2, 2^3-1]$. So we need to allocate all the 5 numbers of 1, 4, 5, 6, and 7 to the nodes of the odd layer. As shown below:
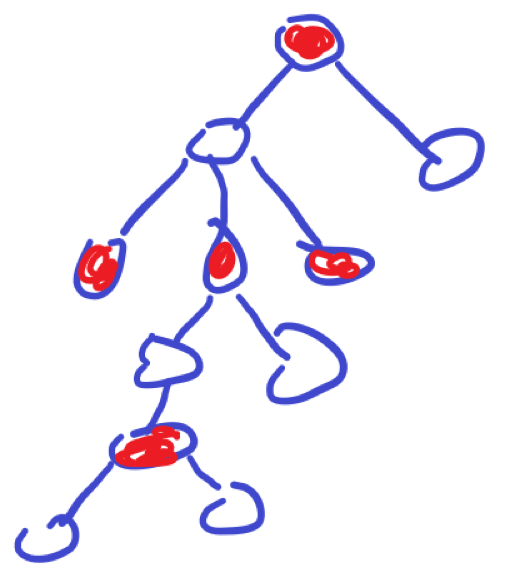
We only need to allocate 5 numbers to the red nodes.
Obviously, the same approach can also be applied to nodes with even depths. Therefore, if the number of nodes with odd depth is more than half, we can select nodes with even depth to do the same operation.
And once the number of nodes that need to be selected is less than half, we must be able to find the corresponding number based on the required number of binary.
For example, 6 numbers are required, and the binary value of 6 is 110. Then we choose $[2^1, 2^2-1]$ and $[2^2, 2^3-1]$.
Code:
Java

C++

