Codeforces Round #753 ABCDEFGH Solutions (Java/C++)

A. Linear Keyboard

Solution:

Just simulate according to the question.

Code:

Java

C++

B. Odd Grasshopper

Solution:

It is not difficult to find that after every 4 jumps, it will definitely return to the original point.

Take $x_0$ being an odd number as an example: $x_1=x_0+1$ must be an even number. $x_2=x_1-2$ is also an even number. $x_3=x_2-3$ must be an odd number. $x_4=x_3+4$ must be an odd number, and $x_4=x_0$.

Code:

Java

C++

C. Minimum Extraction

Solution:

Because each operation is to make the same change to all the numbers. Therefore, the minimum value selected each time is selected by the same order from small to large at the beginning.

So only need to simulate and calculate sequentially after sorting.

Code:

Java

C++

D. Blue-Red Permutation

Solution:

Consider the color distribution of a certain "Yes" case as shown in the figure below. It is not difficult for us to find that we must can continue to operate 3 and 7 so that the left side is all blue and the right side is all red.

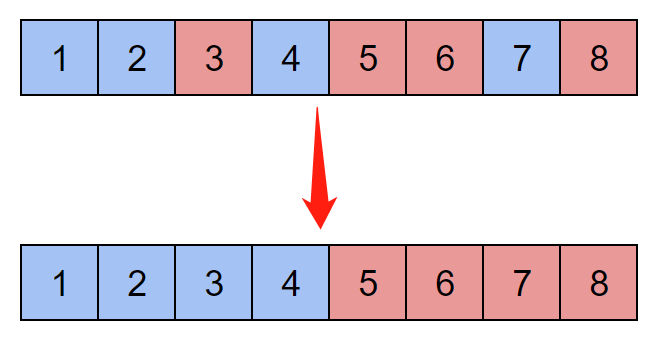
Therefore, we only need to sort the blue and red separately and place them to the far left and right. In the process, if we find that there is a conflict, it means that there must be no solution, just output No.

Code:

Java

C++

E. Robot on the Board 1

Solution:

We start from (1,1) and execute the command according to the order. During the execution, we record the range of points visited. Once the range is found to exceed n and m, then stop execution.

Code:

Java

C++

F. Robot on the Board 2

Personally do not recommend this problem. If you don't have AC, it is recommended to skip this question.

Click the link above for detail solution

G. Banquet Preparations 1

We can calculate the value range of a in each dish according to the value of m, and then determine the value of a according to the remaining total weight.

Codeforces Round #753 Banquet Preparations 1 Solution (Java/C++)

Solution:We represent the total remain weight of each dish by $remain_i$, which obviously has $remain_i=a_i+b_i-m$.

xloypaypa's Blogxloypaypa

Click the link above for detail solution

H. Banquet Preparations 2

Similar to problem G, according to the value range of a, we find that if the value ranges of two a do not intersect, they must be two different dishes. So discretization is enough.

Codeforces Round #753 Banquet Preparations 2 Solution (Java/C++)

Solution:Obviously, if two dishes are the same, then the total weight of the two dishes must also be the same. According to the previous question, we know that we can calculate the value range of the last remaining a.

xloypaypa's Blogxloypaypa

Click the link above for detail solution