Solution:
First of all, because after reaching 0, there will be no slip. Therefore, we consider slip as part of the ability to jump. So we redefine the behavior of a jump, and change the slip after jumping into slip first and then jumping.
So, naturally, from any position i, the range that can jump is: $[i-b[i]-a[i-b[i]], i-b[i]]$.
Suppose we jump to 4 meters from a certain position. At this time, according to the definition of the problem, it should be down 1 meter. So the next jump is from 5 meters. But according to the new definition, we don’t have to slide down, but say, “Starting from 4 meters, we can jump from 0 to 5 meters.”
The significance of doing this is: 1. No need to consider the slip. 2. Starting from any position, you can jump to a continuous interval. 3. The right value of this interval must be greater than the current position (because $b[i]\geq 0$).
We consider the position which before reaching 0 meters. Assume that there are two positions that can reach 0 with one jump. We use x and y to denote these two positions, where x is closer to 0 than y.
So we can clearly find from the figure below that y can not only jump to 0 meters, but also jump to the position of x. (The yellow part in the figure represents the range that can be jumped from x, and the red part represents the range that can be jumped from y)
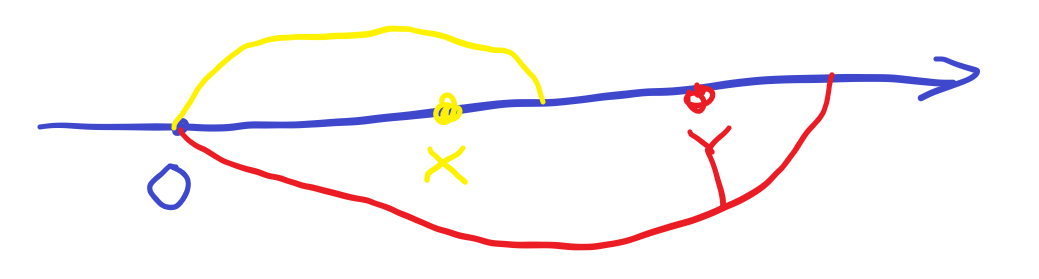
In the same way, we consider the point where we can jump to x and y (that is, we consider the second last jump). It is not difficult to find that if we can jump to x, we must also can jump to y.
So naturally, we start from now=0 and find the farthest one of the points that can jump to now every time. Until now=n.
The remaining problem is how to find all the points that can jump to now. We can use a similar way of pairing parentheses to discretize the jumpable range of each point on the number line.
Code:
Java

C++

