Solution:
Let's take k=3, n=10 as an example, consider the choice of [l1, r1], consider the following two choices: [4, 6] and [3, 5].
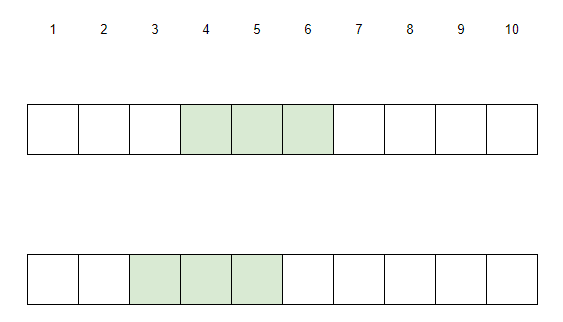
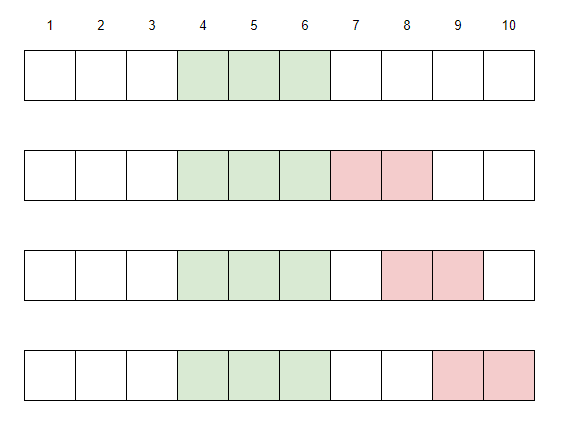
We first consider the feasibility of [4, 6]. According to the description of the problem, [4, 6] needs to find a case where k=2, so that sum(4, 6)<sum(l2,r2), which means that at least one of [7, 8], [8, 9] and [9,10] is feasible, and the sum of the intervals is greater than sum(4, 6). ([9, 10] is obviously impossible)
That is, as shown in the figure below, it is necessary to find a feasible interval and satisfy the conditions among the three red intervals.
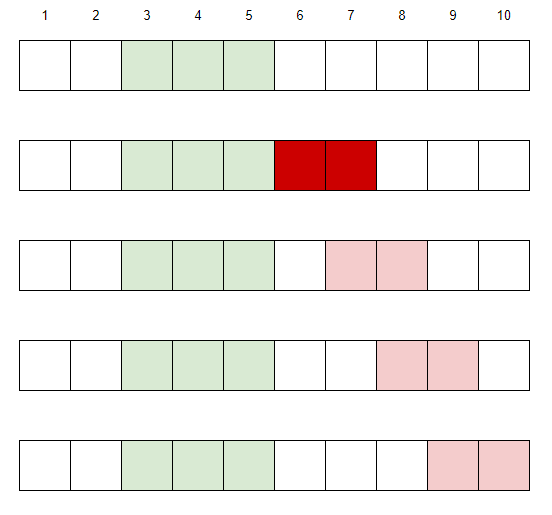
Next, we compare the feasibility of [3, 5]. We get the picture below. It is not difficult to find that the only additional interval considered is the dark red interval.
So it is not difficult to think of the following dp definition: dp[i][j] means that when k=i, for all possible l1>=j, the maximum possible sum(l1, r1). Thus, the following state transition equation:$$
dp[i][j]=\begin{cases}
dp[i][j+1], & \text{if ($sum(j, j+i-1) > dp[i-1][j+i]$)}\\[2ex]
\max(dp[i][j+1], sum(j, j+i-1)), & \text{if ($sum(j, j+i-1) \leq dp[i-1][j+i]$)}
\end{cases}
$$
Finally, there are two points to note:
- Since dp[i][j] is only related to dp[i-1][j], it can be state compressed.
- Pay attention to the value range of j: $0\leq j$ and $\frac {(j+1)*j} 2 \leq n$.
Code:
Java

C++

