Solution:
This question is divided into four parts.
Part 1: Hash
Because there at most m segments of the grid that contain digits 1, So we naturally think of hashing $1\leq l \leq r \leq 10^9$ to $1\leq l \leq r \leq 2\cdot 3\cdot 10^5$. Discrete the two ends of the original segment and sort them, and then hash them in order of size.
The corresponding function in the code is: map_point.
At the same time, here we disperse the m segments into the corresponding rows for convenience in subsequent use.
The corresponding function in the code is: group.
Part 2: DP
we discover. Instead of find the minimum number of rows to be deleted, it is better to find the maximum number of rows that can be constructed. We can naturally think of a DP with $O(n^2)$.
We let $dp[i]$ denote the maximum number of rows that can be constructed with first i lines. So it is natural that $dp[i]=\max(dp[j]+1)$, where $0<j<i$ and line i and line j can be connected.
But obviously, this is the time complexity of $O(n^2)$, and the simplest way to judge whether the i-th line and the j-th line are connected each time is $O(m)$.
Part 3: Segment tree
First of all, we think about the conditions for whether the i-th row and the j-th row are connected? If the i-th row and the j-th row are connected, at least one of column in the two rows is 1 at the same time.
Therefore, if we query the maximum value of the segment in i-th row for all segment in j-th row, and if the query result of a certain segment is not 0, then i and j must have something in common.
Take the following picture as an example:

j will query [0,1] and [5,6] in i, where the query result of [0,1] is 1, and the query result of [5,6] is 0. Therefore, at least one of column in the i-th row and j-th row are 1 at the same time.
Further, we combined the above DP part, we found that a similar method can be used.
For $dp[i]$, our core problem is to find a row j before i so that $dp[i]$ is as large as possible, and i and j have a common 1.
So whenever we find a new dp[i], we update the position of 1 in row i to the segment tree, and the updated value is dp[i]. Where the segment tree maintain the maximum value for the segments.
As for how to find the new dp[i], it is obvious. We only need to query all the segments in row i that are 1 in the segment tree and take the largest value among them.
Take sample 2 as an example:
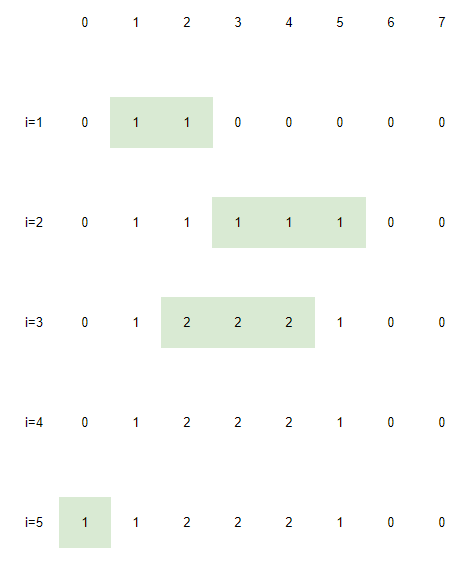
When we ask for dp[3], we can query in i=2 and find that the maximum value that can be queried is 1. So dp[3]=1+1, and then [2-3] is updated to dp[3].
Part 4: Record path
When maintaining the maximum value in the segment tree, it also maintains which row has updated the maximum value of the current interval. In this way, when updating dp[i], record who is the preceding j is. In this way, we can find the longest list in turn, and the remaining elements are to be deleted.
Code:
Java

C++

