Solution:
We can separate the number to 3 categories: odd, even but not include $2^n$ and $2^n$. Then we can get the state transition brought by one step operation:
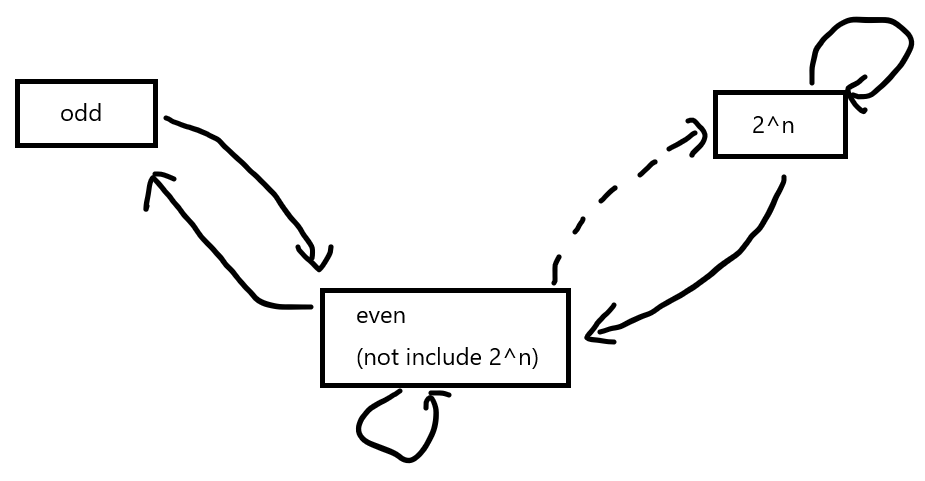
For odd number, after one operation, it must be transferred to even number but not include $2^n$.
Of course, all the factors of this odd number are also odd. Let this odd number to be $a\cdot b$ and $a\cdot b - b=2^x$. Then $(a-1)\cdot b =2^x$. So, $a-1=2^y$ and $b=2^{(x-y)}$ which contradicts that b is an odd number.
For the even number but not include $2^n$, let this number to be $a\cdot b \cdot c$, where a is a even number, b is a odd number and c can be any number. So, $a\cdot b \cdot c-b$ is a odd and $a\cdot b \cdot c-a$ is even.
So, we can see that, if someone get an odd number on his round, there is no other operations, this number must be transferred to the even number (not include $2^n$).
And we know the even number at least can apply one operation. Only prime odd number cannot do operation. So, someone who get even number, he will change it to odd number. Continue this, can get win.
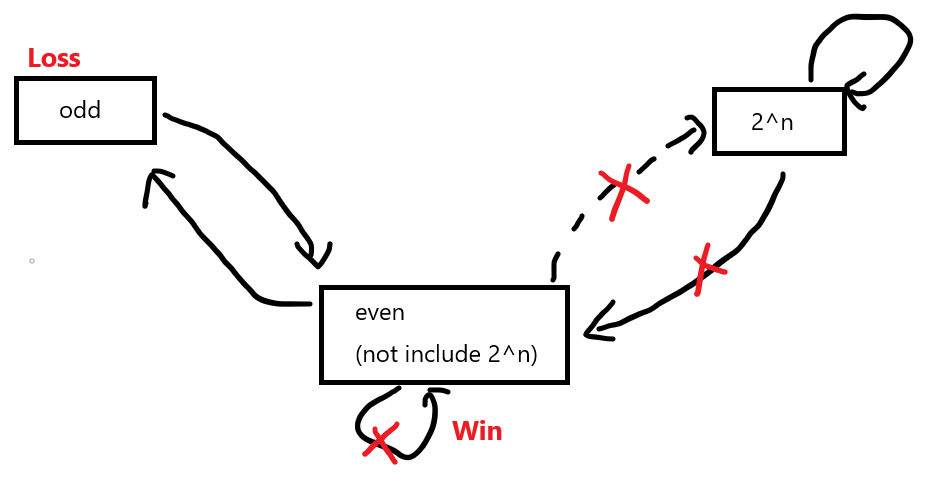
So, if Alice gets an even number (not include $2^n$), then Alice win, otherwise Bob win.
For $2^n$, it can transfer to even number which not $2^n$. But people who get the even number (not include $2^n$) will win. So, people will not do this.
So, people will try to keep it as $2^x$. So, every time, it subtracts $2^{n-1}$. Then the result depends on the parity of the exponential power.
The summary is, for Alice, the status like this:
Code:
Java

C++

