Codeforces Round #719 Solutions

A. Do Not Be Distracted!

Solution:

Scan the string. When we found a new letter, we skip the continually same letter. And mark this letter should not present again. If it presents again, then output "NO".

Code:

B. Ordinary Numbers

Solution:

Construct beautiful numbers within 9 digits from 1-9. Count the number if it less than n.

Code:

C. Not Adjacent Matrix

Solution:

Fill in the numbers along the diagonal. Take $ n = 5 $ as an example:

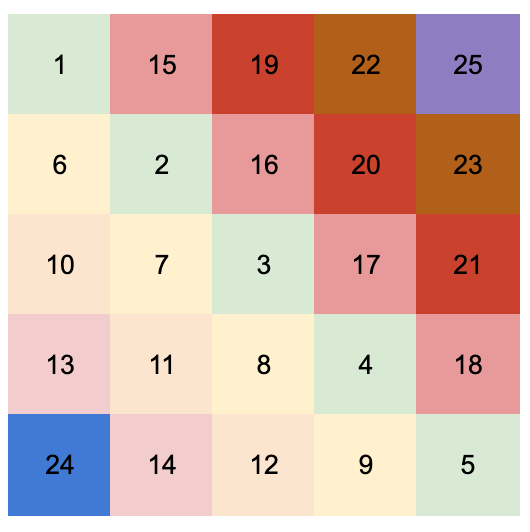
Code:

D. Same Differences

Solution:

Transform the equation, then we get $a_j - j = a_i - i$. So, scan the array, count the number of every $a_x - x$. And calculate the sum of $C_n^2$.

Code:

E. Arranging The Sheep

In fact, it depends on how many sheep go to the left and how many sheep go to the right.

Codeforces Round #719 Arranging The Sheep - Sort

Solution:We define the data structure below: static class Sheep { int suppose_pos, pos;}suppose_pos represent the position of this su

xloypaypa's Blogxloypaypa

F. Guess the K-th Zero (Easy/Hard Version)

Binary search. Query the range $[1,mid]$. But it will change the number in hard version. And we need plus one for some of our caches. So, of course, it's a segment tree problem.

Codeforces Round #719 Guess the K-th Zero (Hard version) - Segment tree

SolutionBase on the easy version, we still binary search in the hard version. So, we query the sum of $[1, mid]$.Now the problem is, after each time, we need change the element from 0 to 1.

xloypaypa's Blogxloypaypa

G. To Go Or Not To Go?

I solved similar problem before. Do BFS from starting and ending point first. Then we consider if use the transport portal or not. I remember last time, I also get TLE by using Dijkstra.

Codeforces Round #719 To Go Or Not To Go? - BFS

Solution:This is a shortest paths problem. But do not use Dijkstra or SPFA to solve this problem. Because the time complex is $O(nm\cdot log(nm))$. Can get TLE with an extra $log$.

xloypaypa's Blogxloypaypa