Solution:
Let me talk about the conclusion first.
For all pairs of points, we sort it from largest to smallest. Query the reachability of the points with higher in-degree to lower in-degree in these pairs in turn. If reachable, then these two point is the answer.
It is obvious after looking at the picture below:
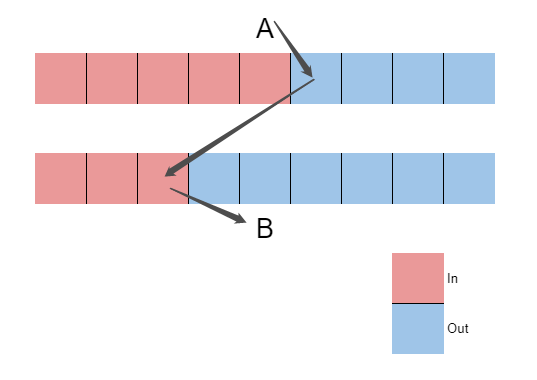
We can found that: At least one of the out-degree points of $B$ must be the in-degree of $A$. So A point with a larger in-degree can reach a smaller point, and it must be a circle.
For two points with same in-degree. It's same, because it will take a in-degree point from $A$, and take a out-degree from $B$.
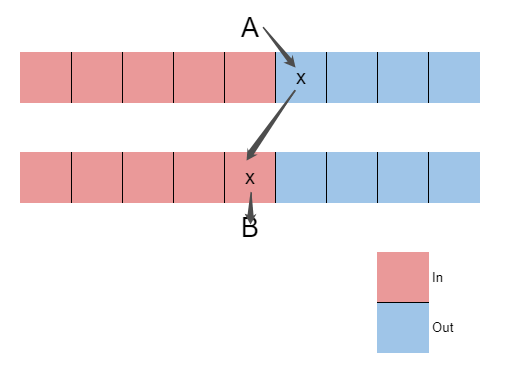
Code:
Submission #113086430 - Codeforces
Codeforces. Programming competitions and contests, programming community

